Lumifuge/Lumisizer/Lumireader - How to determine the position of the bottom of the measuring cells and How to determine volumes (sediment, cream )

The detection principle of the Lumifuge/Lumisizer and Lumireader instruments allows to determine the local position with high precision.

For more advanced applications (determination of sediment heights for example) the knowledge of the position of the bottom of the measuring cells might be necessary. To determine the packing density or to determine the phase ratio of phases separated, it is straight forward to determine these values after calibration by inserting the values obtained for the respective position into an equation.

How to do the calibration ?

The procedure to follow is based on two simple facts

• mass of samples can be easily measured with high precision
• the position of the air-liquid interface is easily obtained from the transmission profiles, see below

#1 For a given type of measuring cells, i.e. rectangular plastic cells or glass cells, a set of samples are filled to different heights with water (density equals 1 g / cm³) with the sample mass determined by a semi-analytical balance (± 1 mg).

#2 Transmission profiles of these samples are obtained using the Lumifuge (up to eight samples per measurement) or the Lumireader.

#3 The position of the interface air-water is determined for each sample

#4 Via fitting a convenient equation the dependence volume-position and position-volume can be obtained, which also gives the position relating to ‘zero volume’, i.e. the position at the bottom

Example – calibration of the Lumireader 4160-101 – rectangular plastic cells

Ten sample cells were filled with water (range 25 mg – 825 mg). For the transmission profiles obtained, see two examples below for 151 and 407 mg, respectively.

For round glass cells with a diameter of 10 mm a range of 150 mg to 5000 mg would be appropriate.

For the Lumifuge with a shorter line detector a range of 20 to 400 mg and 200 – 2700 mg, respectively, is applicable.

One has to take care of the precise placing of the sample cells.

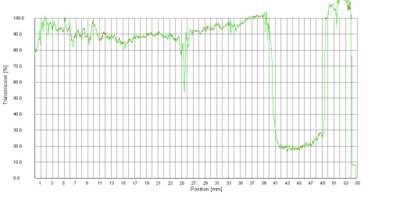
Transmission profiles obtained with the Lumireader 4160-101, plastic rectangular cells, polycarbonate, filled with water 151 (upper figure) and 407 mg (lower figure).

The drop in transmission around position 49 mm (given as distance from the upper end of the CCD line sensor) is caused by the bottom of the cell, however, its position cannot be deduced exactly.

The position of the interface air-water (sharp incline) reads 40.1 and 25.6 mm for the samples with 151 mg (upper figure) and with 407 mg (lower figure), respectively.

These positions correspond to 151 and 407 mm³, respectively.

For the following set of data the results are depicted below


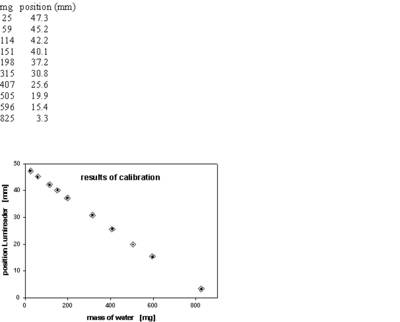
calibration data and plot

Fitted with the equation of type y = a + bx + cx² (eq. 1) one gets

a = 48.78 (position of the cell bottom, i.e. 48.8 mm)

b = - 0.05895

c = 0.000004603

Please note, this is the relation of position as function of the sample mass.

For the determination of volume in relation to the position, however, one needs an equation to compute the volume by inserting the values determined for the position.

The same type of fitting equation might be used as above y = a + bx + cx² (eq. 2)

with y for volume (mm³ or µl) and x for the position.

The regression results in

a = 888.7 (maximum volume traceable, i.e. 888 mm³)

b = -19.56

c = 0.02762

With the knowledge of these parameters and the equation above (eq. 2) one can compute any volume of sediment or the volume of the whole sample. The value of a cream layer or a floating oil layer can be determined by subtracting the volume relating to the position of the interface from the volume of the whole sample accordingly.

Example – Determination of sediment volume and packing density

Below the transmission profile of a flocculated sample of colloidal silica which was measured at gravity to deduce the change in packing density after compaction in a centrifugal field.

Transmission profiles of a flocculated sample of colloidal silica after compaction in a centrifugal field.

The position of the interface air-water is at 25.6 mm relating to a volume of 406 mm³, the position of the sediment interface is at 40.3 mm corresponding to 145 mm³. The layer of water above the sediment, therefore, has a volume of 261 mm³.

The packing density of silica can be expressed in terms of volume fraction:

F = m/(rV) (eq. 3)

with the mass of silica m (in this case 10 mg), a density r of 2.3 g/cm³ or mg/mm³ and the volume of silica V (145 mm³, see above).

According equation (3) the packing density of silica measured results in a volume fraction F of 0.03, very far from a dense packing.